Tag: statistics

How Do Newly Promoted Clubs Survive In The EPL?

Part 2: The Four Survival KPIs

The first part of this two-part consideration of the prospects of newly promoted clubs surviving in the English Premier League (EPL) concluded that the lower survival rate in recent seasons was due to poorer defensive records rather than any systematic reduction in wage expenditure relative to other EPL clubs. It was also suggested that there might be a Moneyball-type inefficiency with newly promoted teams possibly allocating too large a proportion of their wage budget to over-valued strikers when more priority should be given to improving defensive effectiveness. In this post, the focus is on identifying four key performance indicators (KPIs) for newly promoted clubs that I will call the “survival KPIs”. These survival KPIs are then combined using a logistic regression model to determine the current survival probabilities of Burnley, Leeds United and Sunderland in the EPL this season.

The Four Survival KPIs

The four survival KPIs are based on four requirements for a newly promoted club:

  • Squad quality measured as wage expenditure relative to the EPL median
  • Impetus created by a strong start to the season measured by points per game in the first half of the season
  • Attacking effectiveness measured by goals scored per game
  • Defensive effectiveness measured by goals conceded per game

Using data on the 89 newly promoted clubs in the EPL from seasons 1995/96 – 2024/25, these clubs have been allocated to four quartiles for each survival KPI. Table 1 sets out the range of values for each quartile, with Q1 as the quartile most likely to survive through to Q4 as the quartile most likely to be relegated. Table 2 reports the relegation probabilities for each quartile for each KPI. So, for example, as regards squad quality, Table 1 shows that the top quartile (Q1) of newly promoted clubs had wage costs at least 79.5% of the EPL median that season. Table 2 shows that only 22.7% of these clubs were relegated. In contrast, the clubs in the lowest quartile (Q4) had wage costs less than 55% of the EPL median that season and 77.3% of these clubs were relegated.

Table 1: Survival KPIs, Newly Promoted Clubs in the EPL, 1995/96 – 2024/25

Table 2: Relegation Probabilities, Newly Promoted Clubs in the EPL, 1995/96 – 2024/25

The standout result is the low relegation probability for newly promoted clubs in Q1 for the Impetus KPI. Only 8% of newly promoted clubs with an average of 1.21 points per game or better in the first half of the season have been relegated. This equates to 23+ points after 19 games. Only 17 newly promoted clubs have achieved 23+ points by mid-season in the 30 seasons since 1995 and only two have done so in the last five seasons – Fulham in 2022/23 with 31 points and the Bielsa-led Leeds United with 26 points in 2020/21.

It should be noted that there is little difference in the relegation probabilities between Q2 and Q3, the mid-range values for both Squad Quality and Attacking Effectiveness, suggesting that marginal improvements in both of these KPIs have little impact for most clubs. As regards defensive effectiveness, both Q1 and Q2 have low relegation quartiles suggesting that the crucial benchmark is limiting goals conceded to under 1.61 goals per game (or 62 goals conceded over the entire season). Of the 43 newly promoted clubs that have done so since 1995, only seven have been relegated, a relegation probability of 16.3%. Reinforcing the main conclusion from the previous post that the main reason that for the poor performance of newly promoted clubs in recent seasons, only four clubs have conceded fewer than 62 goals in the last five seasons – Fulham (53 goals conceded, 2020/21), Leeds United (54 goals conceded, 2020/21); Brentford (56 goals conceded, 2021/22) and Fulham (53 goals conceded, 2022/23) – with of these four clubs, only Fulham being relegated in 2020/21 (primarily due to their poor attacking effectiveness).

Where Did The Newly Promoted Clubs Go Wrong Last Season?

Just as in the previous season 2023/24, so too last season, all three newly promoted clubs – Ipswich Town, Leicester City and Southampton – were relegated. Table 3 reports the survival KPIs for these clubs. In the case of Ipswich Town, their Squad Quality was low with relative expenditure under 50% of the EPL median. In contrast Leicester City spent close to the EPL median and Southampton were just marginally under the Q1 threshold. The Achilles Heel for all three clubs was their very poor defensive effectiveness, conceding goals at a rate of over two goals per game. Only 11 newly promoted clubs have conceded 80+ goals since 1995; all have been relegated.

Table 3: Survival KPIs, Newly Promoted Clubs in the EPL, 2024/25

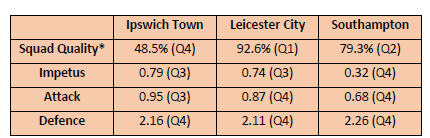
*Calculated using estimated squad salary costs sourced from Capology (www.capology.com)

What About This Season?

As I write, seven rounds of games have been completed in the EPL. Of the three newly promoted clubs, the most impressive start has been by Sunderland who are currently 9th in the EPL with 11 points which puts them in Q1 in terms of Impetus as does their Squad Quality with wage expenditure estimated at 83% of the EPL median, and their defensive effectiveness with only six goals conceded in their first seven games. Leeds United have also made a solid if somewhat less spectacular start with 8 points and ranking in Q2 for all four survival KPIs. Both Sunderland and Leeds United are better placed at this stage of the season than all three newly promoted clubs last season when Leicester City had 6 points, Ipswich Town 4 points and Southampton 1 point. Burnley have made the poorest start of the newly promoted clubs this season with only 4 points, matching Ipswich Town’s start last season but, unlike Ipswich Town, Burnley rank Q2 in both Squad Quality and Attack. Worryingly Burnley’s defensive effectiveness which was so crucial to their promotion from the Championship has been poor so far this season and, at over two goals conceded per game, on a par with Ipswich Town, Leicester City and Southampton last season.

Table 4: Survival KPIs and Survival Probabilities, Newly Promoted Clubs in the EPL, 2025/26, After Round 7

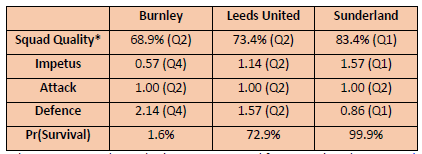
*Calculated using estimated squad salary costs sourced from Capology (www.capology.com)

Using the survival KPIs for all 86 newly promoted clubs 1995 – 2024, a logistic regression model has been estimated for the survival probabilities of newly promoted clubs in the EPL. This model combines the four survival KPIs and weights their relative importance based on their ability to jointly identify correctly those newly promoted clubs that will survival. The model has a success rate of 82.6% predicting which newly promoted clubs will survive and which will be relegated. Based on the first seven games, Sunderland have a survival probability of 99.9%, Leeds United 72.9% and Burnley 1.6%. These figures are extreme and merely highlight that Sunderland have made an exceptional start, Leeds United a good start and Burnley have struggled defensively. It is still early days and crucially the survival probabilities do not control for the quality of the opposition. Sunderland have yet to play a team in the top five whereas Leeds United and Burnley have both played three teams in the top five. I will update these survival probabilities regularly as the season progresses. They are likely to be quite volatile in the coming weeks but should become more stable and robust by late December.

Diagnostic Testing Part 2: Spatial Diagnostics

Analytical models takes the following general form:

Outcome = f(Performance, Context) + Stochastic Error

The structural model represents the systematic (or “global”) variation in the process outcome associated with the variation in the performance and context variables. The stochastic error acts as a sort of “garbage can” to capture “local” context-specific influences on process outcomes that are not generalisable in any systematic way across all the observations in the dataset. All analytical models assume that the structural model is well specified and the stochastic error is random. Diagnostic testing is the process of checking that these two assumptions hold true for any estimated analytical model.

Diagnostic testing involves the analysis of the residuals of the estimated analytical model.

Residual = Actual Outcome – Predicted Outcome

Diagnostic testing is the search for patterns in the residuals. It is a matter of interpretation as to whether any patterns in the residuals are due to structural mis-specification problems or stochastic error mis-specification problems. But structural problems must take precedence since, unless the structural model is correctly specified, the residuals will be biased estimates of the stochastic error since they will be contaminated by structural mis-specification. In this post I am focusing on structural mis-specification problems associated with cross-sectional data in which the dataset comprises observations of similar entities at the same point in time. I label this type of residual analysis as “spatial diagnostics”. I will utilise all three principal  methods for detecting systematic variation in residuals: residual plots, diagnostic test statistics, and auxiliary regressions.

Data

The dataset being used to illustrate spatial diagnostics was originally extracted from the Family Expenditure Survey in January 1993. The dataset contains information on 608 households. Four variables are used – weekly household expenditure (EXPEND) is the outcome variable to be modelled by weekly household income INCOME), the number of adults in the household (ADULTS) and the age of the head of the household (AGE) which is defined as whoever is responsible for completing the survey. The model is estimated using linear regression.

Initial Model

The estimated linear model is reported in Table 1 below. On the face of it, the estimated model seems satisfactory, particularly for such a simple cross-sectional model, with around 53% of the variation in weekly expenditure being explained statistically by variation in weekly income, the number of adults in the household and the age of the head of household (R2 = 0.5327). All three impact coefficients are highly significant (P-value < 0.01). The t-statistic provides a useful indicator of the relative importance of the three predictor variables since it effectively standardises the impact coefficients using their standard errors as a proxy for the units of measurement. Not surprisingly, weekly household expenditure is principally driven by weekly household income with, on average, 59.6p spent out of every additional £1 of income.

Diagnostic Tests

However, despite the satisfactory goodness of fit and high statistical significance of the impact coefficients, the linear model is not fit for purpose in respect of its spatial diagnostics. Its residuals are far from random as can be seen clearly in the two residual plots in Figures 1 and 2. Figure 1 is the scatterplot of the residuals against the outcome variable, weekly expenditure. The ideal would be a completely random scatterplot with no pattern in either the average value of the residual which should be zero (i.e. no spatial correlation) or in the degree of dispersion (known as “homoskedasticity”). In other words, the scatterplot should be centred throughout on the horizontal axis and there should also be a relatively constant vertical spread of the residual around the horizontal axis. But the residuals for the linear model are clearly trended upwards in both value (i.e. spatial correlation) and dispersion (i.e. heteroskedasticity). In most cases in my experience this sort of pattern in the residuals is caused by wrongly treating the core relationship as linear when it is better modelled as a curvilinear or some other form of non-linear relationship.

            Figure 2 provides an alternative residual plot in which the residuals are ordered by their associated weekly expenditure. Effectively this plot replaces the absolute values of weekly expenditure with their rankings from lowest to highest. Again we should ideally get a random plot with no discernible pattern between adjacent residuals (i.e. no spatial correlation) and no discernible pattern in the degree of dispersion (i.e. homoskedasticity). Given the number of observations and the size of the graphic it is impossible to determine visually if there is any pattern between the adjacent residuals in most of the dataset except in the upper tail. But the degree of spatial correlation can be measured by applying the correlation coefficient to the relationship between ordered residuals and their immediate neighbour. Any correlation coefficient > |0.5| represents a large effect. In the case of the ordered residuals for the linear model of weekly household expenditure the spatial correlation coefficient is 0.605 which provides evidence of a strong relationship between adjacent ordered residuals i.e. the residuals are far from random.

            So what is causing the pattern in the residuals? One way to try to answer this question is to estimate what is called an “auxiliary regression” in which regression analysis is applied to model the residuals from the original estimated regression model. One widely used form of auxiliary regression is to use the squared residuals as the outcome variable to be modelled. The results for this type of auxiliary regression applied to the residuals from the linear model of weekly household regression are reported in Table 2. The auxiliary regression overall is statistically significant (F = 7.755, P-value = 0.000). The key result is that there is a highly significant relationship between the squared residuals and weekly household income, suggesting that the next step is to focus on reformulating the income effect on household expenditure.

Revised Model and Diagnostic Tests

So diagnostic testing has suggested the strong possibility that modelling the income effect on household expenditure as a linear effect is inappropriate. What is to be done? Do we need to abandon linear regression as the modelling technique? Fortunately the answer is “not necessarily”. Although there are a number of non-linear modelling techniques, it is in most cases possible to continue using linear regression by transforming the original variables. Instead of changing the estimation method, the alternative is to transform the original variables such that there is a linear relationship between the transformed variables that is amenable to estimation by linear regression. One commonly used transformation is to introduce the square of a predictor alongside the original predictor to capture a quadratic relationship. Another common transformation is to convert the model into a loglinear form by using logarithmic transformations of the original variables. It is the latter approach that I have used as a first step in attempting to improve the structural specification of the household expenditure model. Specifically, I have replaced the original expenditure and income variables, EXPEND and INCOME, with their natural log transformations, LnEXPEND and LnINCOME, respectively. The results of the regression analysis and diagnostic testing of the new loglinear model are reported below.

The estimated regression model is broadly similar in respect of its goodness of fit and statistical significance of the impact coefficients although, given the change in the functional form, these are not directly comparable. The impact coefficient on LnINCOME is 0.674 which represents what economists term “income elasticity” and implies that, on average, a 1% change in income is associated with a 0.67% change in expenditure in the same direction. The spatial diagnostics have improved although the residual scatterplot still shows evidence of a trend. The ordered residuals appear much more random than previously with the spatial correlation coefficient having been nearly halved and now evidence only of a medium-sized effect (> |0.3|) between adjacent residuals. The auxiliary regression is still significant overall (F = 6.204; P-value = 0.000) and, although the loglinear specification has produced a better fit for the income effect (with a lower t-statistic and increased P-value), it has had an adverse impact on the age effect (with a higher t-statistic and a P-value close to being significant at the 5% level). The conclusion – the regression model of weekly household expenditure remains “work in progress”. The next steps might be to consider extending the log transformation to the other predictors and/or introducing a quadratic age effect.

Other Related Posts

Diagnostic Testing Part 1: Why Is It So Important?

Measuring Trend Growth

Executive Summary

  • The most useful summary statistic for a trended variable is the average growth rate
  • But there are several different methods for calculating average growth rates that can often generate very different results depending on whether all the data is used or just the start and end points, and whether simple or compound growth is assumed
  • Be careful of calculating average growth rates using only the start and end points of trended variables since this implicitly assumes that these two points are representative of the dynamic path of the trended variable and may give a very biased estimate of the underlying growth rate
  • Best practice is to use all of the available data to estimate a loglinear trendline which allows for compound growth and avoids having to calculate an appropriate midpoint of a linear trendline to convert the estimated slope into  growth rate

When providing summary statistics for trended time-series data, the mean makes no sense as a measure of the point of central tendency. By definition, there is no point of central tendency in trended data. Trended data are either increasing or decreasing in which case the most useful summary statistic is the average rate of growth/decline. But how do you calculate the average growth rate? In this post I want to discuss the pros and cons of the different ways of calculating the average growth rate, using total league attendances in English football (the subject of my previous post) as an illustration.

              There are at least five different methods of calculating the average growth rate:

  1. “Averaged” growth rate: use gt = (yt – yt-1)/yt-1 to calculate the growth rate for each period then average these growth rates
  2. Simple growth rate: use the start and end values of the trended variable to calculate the simple growth rate with the trended variable modelled as yt+n = yt(1 + ng)
  3. Compound growth rate: use the start and end values of the trended variable to calculate the compound growth rate with the trended variable modelled as yt+n = yt(1 + g)n
  4. Linear trendline: estimate the line of best fit for yt = a + gt (i.e. simple growth)
  5. Loglinear trendline: estimate the line of best fit for ln yt = a + gt (i.e. compound growth)

where y = the trended variable; g  = growth rate; t = time period; n = number of time periods; a = intercept in line of best fit

These methods differ in two ways. First, they differ as to whether the trend is modelled as simple growth (Methods 2, 4) or compound growth (Methods 3, 5). Method 1 is effectively neutral in this respect. Second, the methods differ in terms of whether they use only the start and end points of the trended variable (Methods 2, 3) or use all of the available data (Methods 1, 4, 5). The problem with only using the start and end points is that there is an implicit assumption that these are representative of the underlying trend with relatively little “noise”. But this is not always the case and there is a real possibility of these methods biasing the average growth rate upwards or downwards as illustrated by the following analysis of the trends in football league attendances in England since the end of the Second World War.

Figure 1: Total League Attendances (Regular Season), England, 1946/47-2022/23

This U-shaped timeplot of total league attendances in England since the end of the Second World War splits into two distinct sub-periods of decline/growth:

  • Postwar decline: 1948/49 – 1985/86
  • Current revival: 1985/86 – 2022/23

Applying the five methods to calculate the average annual growth rate of these two sub-periods yields the following results:

MethodPostwar Decline 1948/49 – 1985/86Current Revival 1985/86 – 2022/23*
Method 1: “averaged” growth rate-2.36%2.28%
Method 2: simple growth rate-1.62%3.00%
Method 3: compound growth-2.45%2.04%
Method 4: linear trendline-1.89%1.75%
Method 5: loglinear trendline-1.95%1.85%
*The Covid-affected seasons 2019/20 and 2020/21 have been excluded from the calculations of the average growth rate.

What the results show very clearly is the wide variability in the estimates of average annual growth rates depending on the method of calculation. The average annual rate of decline in league attendances between 1949 and 1986 varies between -1.62% (Method 2 – simple growth rate) to -2.45% (Method 3 – compound growth rate). Similarly the average annual rate of growth from 1986 onwards ranges from 1.75% (Method 4 – linear trendline) to 3.00% (Method 2 – simple growth rate). To investigate exactly why the two alternative methods for calculating the simple growth rate during the Current Revival give such different results, the linear trendline for 1985/86 – 2022/23 is shown graphically in Figure 2.

Figure 2: Linear Trendline, Total League Attendances, England, 1985/86 – 2022/23

As can be seen, the linear trendline has a high goodness of fit (R2 = 93.1%) and the fitted endpoint is very close to the actual gate attendance of 34.8 million in 2022/23. However, there is a relatively large divergence at the start of the period with the fitted trendline having a value of 18.2 million whereas the actual gate attendance in 1985/86 was 16.5 million. It is this divergence that accounts in part for the very different estimates of average annual growth rate generated by the two methods despite both assuming a simple growth rate model. (The rest of the divergence is due to the use of midpoint to convert the slope of the trendline into a growth rate.)

              So which method should be used? My advice is to be very wary of calculating average growth rates using only the start and end points of trended variables. You are implicitly assuming that these two points are representative of the dynamic path of the trended variable and may give a very biased estimate of the underlying growth rate. My preference is always to use all of the available data to estimate a loglinear trendline which allows for compound growth and avoids having to calculate an appropriate midpoint of a linear trendline to convert the estimated slope into a growth rate.

Read Other Related Posts

The Problem with Outliers

Executive Summary

  • Outliers are unusually extreme observations that can potentially cause two problems:
    1. Invalidating the homogeneity assumption that all of the observations have been generated by the same behavioural processes; and
    2. Unduly influencing any estimated model of the performance outcomes
  • A crucial role of exploratory data analysis is to identify possible outliers (i.e. anomaly detection) to inform the modelling process
  • Three useful techniques for identifying outliers are exploratory data visualisation, descriptive statistics and Marsh & Elliott outlier thresholds
  • It is good practice to report estimated models including and excluding the outliers in order to understand their impact on the results

A key function of the Exploratory stage of the analytics process is to understand the distributional properties of the dataset to be analysed. Part of the exploratory data analysis is to ensure that the dataset meets both the similarity and variability requirements. There must be sufficient similarity in the data to make it valid to treat the dataset as homogeneous with all of the observed outcomes being generated by the same behavioural processes (i.e. structural stability). But there must also be enough variability in the dataset both in the performance outcomes and the situational variables potentially associated with the outcomes so that relationships between changes in the situational variables and changes in performance outcomes can be modelled and investigated.

Outliers are unusually extreme observations that call into question the homogeneity assumption as well as potentially having an undue influence on any estimated model. It may be that the outliers are just extreme values generated by the same underlying behavioural processes as the rest of the dataset. In this case the homogeneity assumption is valid and the outliers will not bias the estimated models of the performance outcomes. However, the outliers may be the result of very different behavioural processes, invalidating the homogeneity assumption and rendering the estimated results of limited value for actionable insights. The problem with outliers is that we just do not know whether or not the homogeneity assumption is invalidated. So it is crucial that the exploratory data analysis identifies possible outliers (what is often referred to as “anomaly detection”) to inform the modelling strategy.

The problem with outliers is illustrated graphically below. Case 1 is the baseline with no outliers. Note that the impact (i.e. slope) coefficient of the line of best fit is 1.657 and the goodness of fit is 62.9%.

Case 2 is what I have called “homogeneous outliers” in which a group of 8 observations have been included that have unusually high values but have been generated by the same behavioural process as the baseline observations. In other words, there is structural stability across the whole dataset and hence it is legitimate to estimate a single line of best fit. Note that the inclusion of the outliers slightly increases the estimated impact coefficient to 1.966  but the goodness of fit increases substantially to 99.6%, reflecting the massive increase in the variance of the observations “explained” by the regression line.

Case 3 is that of “heterogeneous outliers” in which the baseline dataset has now been expanded to include a group of 8 outliers generated by a very different behavioural process. The homogeneity assumption is no longer valid so it is inappropriate to model the dataset with a single line of best fit. If we do so, then we find that the outliers have an undue influence with the impact coefficient now estimated to be 5.279, more than double the size of the estimated impact coefficient for the baseline dataset excluding the outliers. Note that there is a slight decline in the goodness of fit to 97.8% in Case 3 compared to Case 2, partly due to the greater variability of the outliers as well as the slightly poorer fit for the baseline observations of the estimated regression line.

Of course, in this artificially generated example, it is known from the outset that the outliers have been generated by the same behavioural process as the baseline dataset in Case 2 but not in Case 3. The problem we face in real-world situations is that we do not know if we are dealing with Case 2-type outliers or Case 3-type outliers. We need to explore the dataset to determine which is more likely in any given situation.

There are a number of very simple techniques that can be used to identify possible outliers. Three of the most useful are:

  1. Exploratory data visualisation
  2. Summary statistics
  3. Marsh & Elliott outlier thresholds

1.Exploratory data visualisation

Histograms and scatterplots as always should be the first step in any exploratory data analysis to “eyeball” the data and get a sense of the distributional properties of the data and the pairwise relationships between all of the measured variables.

2.Summary statistics

Descriptive statistics provide a formalised summary of the distributional properties of variables. Outliers at one tail of the distribution will produce skewness that will result n a gap between the mean and median. If there are outliers in the upper tail, this will tend to inflate the mean relative to the median (and the reverse if the outliers are in the lower tail). It is also useful to compare the relative dispersion of the variables. I always include the coefficient of variation (CoV) in the reported descriptive statistics.

CoV = Standard Deviation/Mean

CoV uses the mean to standardise the standard deviation for differences in measurement scales so that the dispersion of variables can be compared on a common basis. Outliers in any particular variable will tend to increase CoV relative to other variables.

3. Marsh & Elliott outlier thresholds

Marsh & Elliott define outliers as any observation that lies more than 150% of the interquartile range beyond either the first quartile (Q1) or the third quartile (Q3).

Lower outlier threshold: Q­1 – [1.5(Q3 – Q1)]

Upper outlier threshold: Q­3 + [1.5(Q3 – Q1)]

I have found these thresholds to be useful rules of thumb to identify possible outliers.

Another very useful technique for identifying outliers is cluster analysis which will be the subject of a later post.

So what should you do if the exploratory data analysis indicates the possibility of outliers in your dataset? As the artificial example illustrated, outliers (just like multicollinearity) need not necessarily create a problem for modelling a dataset. The key point is that exploratory data analysis should alert you to the possibility of problems so that you are aware that you may need to take remedial actions when investigating the multivariate relationships between outcome and situational variables at the Modelling stage. It is good practice to report estimated models including and excluding the outliers in order to understand their impact on the results. If there appears to be a sizeable difference in one or more of the estimated coefficients when the outliers are included/excluded, then you should formally test for structural instability using F-tests (often called Chow tests). Testing for structural stability in both cross-sectional and longitudinal/time-series data will be discussed in more detail in a future post. Some argue to drop outliers from the dataset but personally I am loathe to discard any data which may contain useful information. Knowing the impact of the outliers on the estimated coefficients can be useful information and, indeed, it may be that further investigation into the specific conditions of the outliers could prove to be of real practical value.

The two main takeaway points are that (1) a key component of exploratory data analysis should always be checking for the possibility of outliers; and (2) if there are outliers in the dataset, ensure that you investigate their impact on the estimated models you report. You must avoid providing actionable insights that have been unduly influenced by outliers that are not representative of the actual situation with which you are dealing.

Read Other Related Posts

The Keys to Success in Data Analytics

Executive Summary

  • Data analytics is a very useful servant but a poor leader
  • There are seven keys to using data analytics effectively in any organisation:
  1. A culture of evidence-based practice
  2. Leadership buy-in
  3. Decision-driven analysis
  4. Recognition of analytics as a source of marginal gains
  5. Realisation that analytics is more than reporting outcomes
  6. Soft skills are crucial
  7. Integration of data silos
  • Effective analysts are not just good statisticians
  • Analysts must be able to engage with decision-makers and “speak their language”

Earlier this year, I gave a presentation to a group of data analysts in a large organisation. My remit was to discuss how data analytics can be used to enhance performance. They were particularly interested in the insights I had gained from my own experience both in business (my career started as an analyst in the Unilever’s Economics Department in the mid-80s) and in elite team sports. I started off with my basic philosophy that “data analytics is a very useful servant but a poor leader” and then summarised the lessons I had learnt as seven keys to success in data analytics. Here are those seven keys to success.

1.A culture of evidence-based practice

Data analytics can only be effective in organisations committed to evidence-based practice. Using evidence to inform management decisions to enhance performance must be part of the corporate culture, the organisation’s way of doing things. The culture must be a process culture by which I mean a deep commitment to doing things the right way. In a world of uncertainty we can never be sure that what we do will lead to the future outcomes we want and expect. We can never fully control future outcomes. Getting the process right in the sense of using data analytics to make the effective use of all the available evidence will maximise the likelihood of an organisation achieving better performance outcomes.

2. Leadership buy-in

A culture of evidence-based practice can only thrive when supported and encouraged by the organisation’s leadership. A “don’t do as I do, do as I say” approach seldom works. Leaders must lead by example and continually demonstrate and extol the virtues of evidence-based practice. If a leader adopts the attitude that “I don’t need to know the numbers to know what the right thing is to do” then this scepticism about the usefulness of data analytics will spread throughout the organisation and fatally undermine the analytics function.

3. Decision-driven analysis

Data analytics is data analysis for practical purpose. The purpose of management one way or another is to improve performance. Every data analytics project must start with the basic question “what managerial decision will be impacted by the data analysis?”. The answer to the question gives the analytics project its direction and ensures its relevance. The analyst’s function is not to find out things that they think would be interesting to know but rather things that the manager needs to know to improve performance.

4. Recognition of analytics as a source of marginal gains

The marginal gains philosophy, which emerged in elite cycling, is the idea that making a large improvement in performance is often achieved as the cumulative effect of lots of small changes. The overall performance of an organisation involves a myriad of decisions and actions. Data analytics can provide a structured approach to analysing organisational performance, decomposing it into its constituent micro components, benchmarking these micro performances against past performance levels and the performance levels of other similar entities, and identifying the performance drivers. Continually searching for marginal gains fosters a culture of wanting to do better and prevents organisational complacency.

5. Realisation that analytics is more that reporting outcomes

In some organisations data analytics is considered mainly as a monitoring process, tasked with tracking key performance indicators (KPIs) and reporting outcomes often visually with performance dashboards. This is an important function in any organisation but data analytics is much more than just monitoring performance. Data analytics should be diagnostic, investigating fluctuations in performance and providing actionable insights on possible managerial interventions to improve performance.

6. Soft skills are crucial

Effective analysts must have the “hard” skills of being good statisticians, able to apply appropriate analytical techniques correctly. But crucially effective analysts must also have the “soft” skills of being able to engage with managers and speak their language. Analysts must understand the managerial decisions that they are expected to inform, and they must be able to tap into the detailed knowledge of managers. Analysts must avoid being seen as the “Masters of the Universe”. They must respect the managers, work for them and work with them. Analysts should be humble. They must know what they bring to the table (i.e. the ability to forensically explore data) and what they don’t (i.e. experience and expertise of the specific decision context). Effective analytics is always a team effort.

7. Integration of data silos

Last but not least, once data analytics has progressed in an organisation beyond a few individuals working in isolation and storing the data they need in their own spreadsheets, there needs to be a centralised data warehouse managed by experts in data management. Integrating data silos opens up new possibilities for insights. This is a crucial part of an organisation developing the capabilities of an “analytical competitor” which I will explore in my next Methods post.

Read Other Related Posts