Author: Bill Gerrard - Winning With Analytics

The IPL Player Auction

Executive Summary

  • There were three key features of the IPL auction values of players in 2023:
  1. A premium was paid for top Indian talent
  2. High values were attached to top but more risky overseas talent
  3. It cost more to buy runs scored than it did to limit runs conceded
  • Mumbai Indians were the top batting side in 2023 but ranked poorly on bowling hence the expectation that they will focus on strengthening their bowling resources in the 2024 auction
  • This intention has clearly been signalled by the release of a large number of their bowlers and the high-profile trade for the return of Hardik Pandya
  • In any auction there is an ever-present danger of the Winner’s Curse – winning the auction by bidding an inflated market value well in excess of the productive value 

During my recent visit to the Jio Institute in Mumbai, I undertook some research on the player auction in the Indian Premier League (IPL). I also used the IPL as the context to investigate the topics of player ratings and player valuation with my graduate sport management class. The discussion with my students, several of whom had a very good knowledge of the IPL and individual teams and players, was motivated by Billy Beane’s involvement in the IPL as an advisor to the Rajasthan Royals. In a recent conversation with Billy, he commented that cricket is undergoing its own sabermetrics revolution. So the question I set the students – are there any apparent Moneyball-type inefficiencies in the valuation of players in the IPL player auctions, with a specific focus on last year’s auction? And looking ahead, could we predict the strategies that individual teams might adopt in the 2024 auction to be held in Dubai on 19th December?

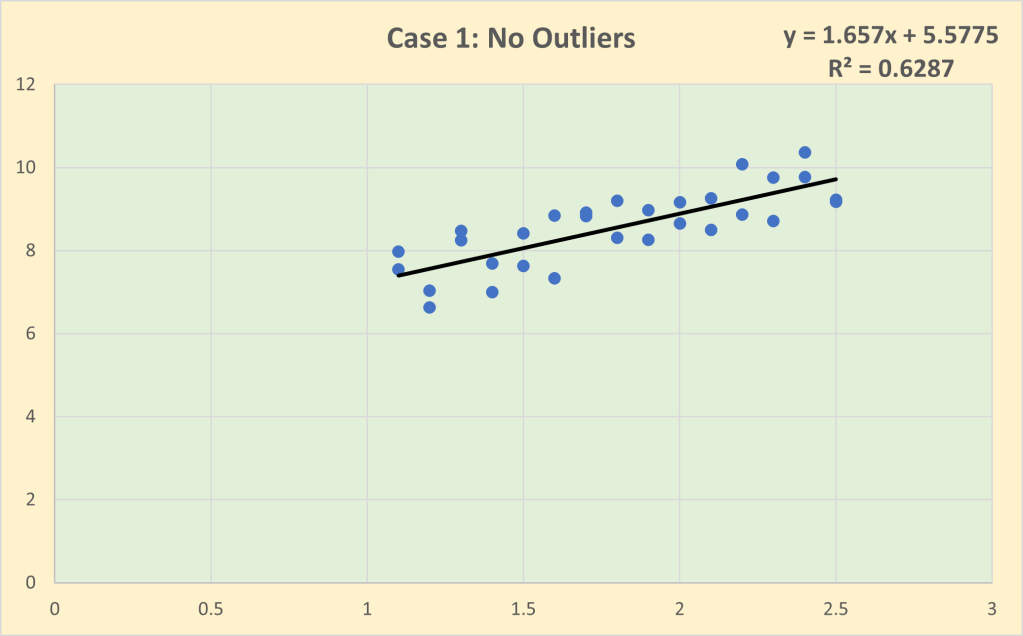
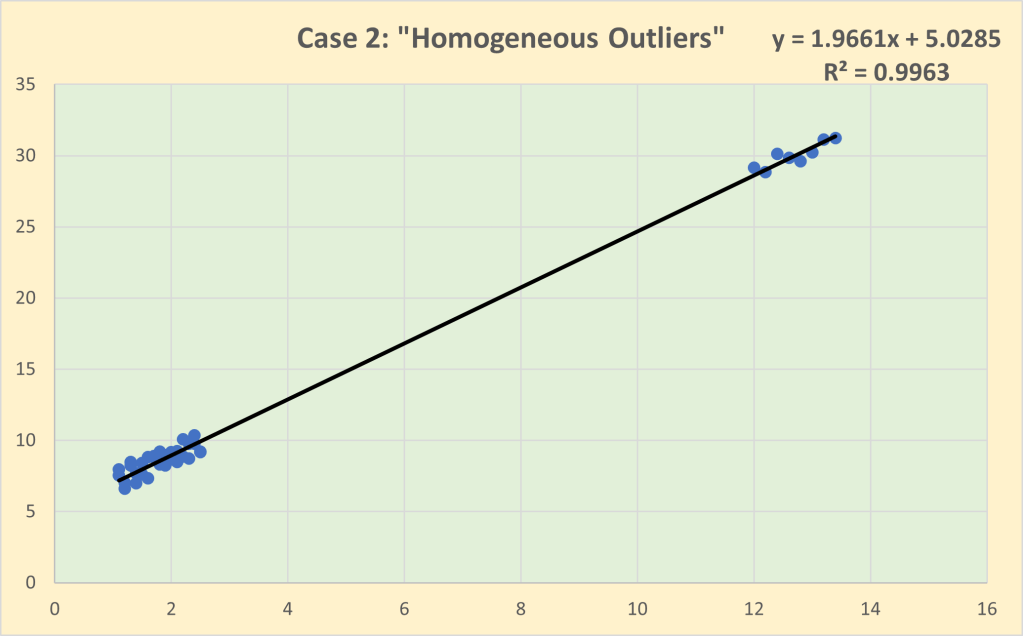
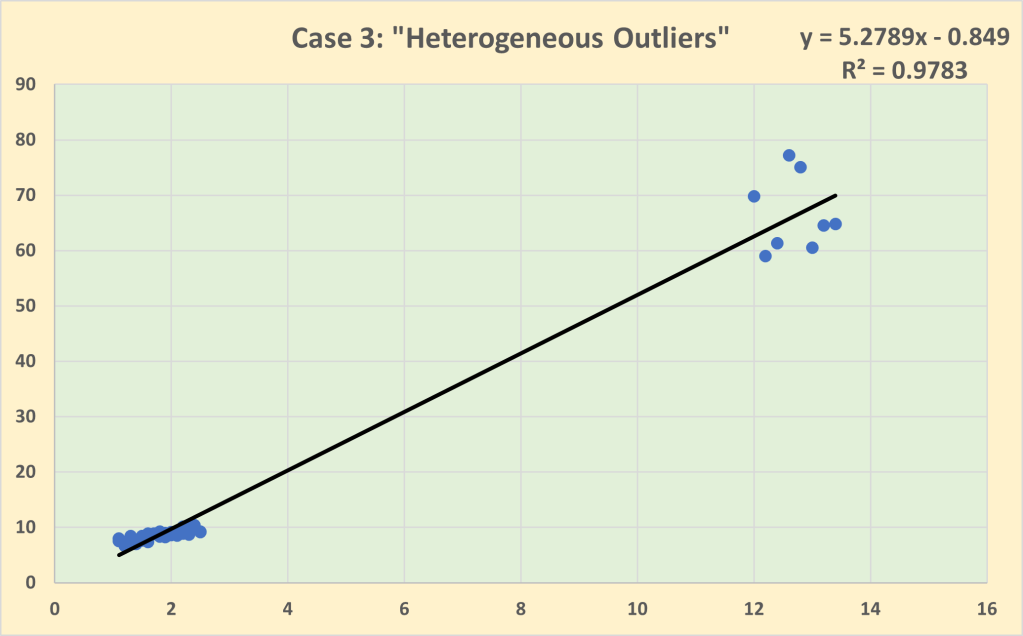
Looking at the 2023 IPL player auction, there appear to be three key features of the player values:

  1. There is a premium paid for top domestic talent when these players become available
  2. High values are attached to top overseas talent but they are higher risk
  3. It costs more to buy runs scored than it does to limit runs conceded

It is no surprise that top Indian players command the highest values – they are experienced and effective in the playing conditions, are big box-office draws, and have high scarcity value. These players are the first on their current team’s retained list and both difficult and expensive to prise them away to another team with a sufficiently lucrative deal for all parties.

As a consequence, teams are forced to focus on the overseas market to find an alternative source for top talent. But this can be a high-risk strategy. Often these players have little or no previous experience in playing in the IPL or even playing in India. Their availability for the whole tournament can be problematic. For example, the IPL overlaps the early part of the English domestic season and top English players are likely to have commitments to the national teams in both test and limited-overs matches. And there is the ever-present risk of injury as the playing schedule extends throughout the whole year. Two of the top valued players in last year’s IPL player auction were Ben Stokes and Harry Brook. Stokes was limited to bowling only one over and had two short innings with the bat before injury ended his IPL season; his obvious priority as captain of the England test team and the inspiration behind the Bazball approach was to get fit for the Ashes series. He has just been released by Chennai Super Kings and has undergone knee surgery in the last few days. Stokes will not be available for the IPL in 2024. Understandably, Harry Brook as an emerging star, commanded one of the highest auction values but his performances in his first season in the IPL were disappointing by his high standards. On my rating system, he ranked only 44th out of the 50 batsmen with 11+ innings but was the 5th highest valued player in the auction. Sunrisers Hyderabad have waived their right to retain his services for the IPL in 2024.

In a number of pro team sports, there is tendency for teams to put a higher value on offensive players who score compared to defensive players who prevent scores being conceded. This is a market inefficiency since a score for has the same weighting as a score against in determining the match outcome. The inefficiency is perhaps more explicable in the invasion-territorial team sports such as the various codes of football since it is more difficult in these sports to separate out the impact of individual player contributions. And, after all, scoring is an observable event whereas defence is about preventing scoring events occurring so there is added uncertainty as to whether or not a score would have been conceded had it not been for a particular defensive action by a player. But this inefficiency is much less explicable in striking-and-fielding team sports such as baseball and cricket where the responsibility for scores conceded can be much more clearly be allocated to individual pitchers/bowlers and fielders. So perhaps a Moneyball-type strategy could be adopted by IPL teams who are weaker in their bowling.

Given that I was based in Mumbai and visiting the Jio Institute which has been established by Reliance Industries who also own the Mumbai Indians franchise, the obvious team to analyse were the Mumbai Indians. I hasten to add that I am not privy to any “inside information” and all of my analysis is based on publicly available data. Table 1 below summarises the batting and bowling performances of the 10 IPL team in 2023.

Table 1: Team Summary Performance, Batting and Bowling, IPL 2023

Note: Runs scored and runs conceded are calculated per ball for all matches (i.e. regular season and end-of-season playoffs). The overall batting and bowling rankings include a number of metrics other than just the scoring and conceding rates.

As can be seen in Table 1, the Mumbai Indians topped the charts in batting but performed relatively poorly in bowling. This suggests that their focus in the coming auction will be on strengthening their bowling. Their intent has clearly been signalled by the release of a large proportion of their bowlers and the high-profile trade for the return of Hardik Pandya.

One final thought as regards the forthcoming IPL player auction. In any auction there is an ever-present danger of the Winner’s Curse – winning the auction by bidding an inflated market value well in excess of the productive value. “Winning the battle, losing the war.” Any bidder in any auction is well advised to have a clear idea of the expected productive value of the future performance of the asset for which they are bidding. In the case of players, it is vital to have a well-grounded estimate of the future value of both the player’s expected incremental contribution on-the-field as well as their image value off-the-field. This should set the upper bound for a team’s bid for their services. As in any acquisition, you are buying the future not the past. Outbid the other teams and you secure the employment contract for the player giving you the rights to the uncertain future performance of the player. Past performance is a guide to possible future performance but you must always factor in the uncertainty inevitably attached to expected future performance.

Football, Finance and Fans in the European Big Five

Executive Summary

  •  Divergent revenue growth paths in the Big Five European football leagues since 1996 has more than doubled the inequality in the financial strength of these leagues.
  • The financial dominance of the EPL is based on growing gate attendances, increasing value of media rights and high marketing efficiency.
  • The financial dominance of the EPL puts it at a massive advantage in attracting the best sporting talent.
  • The pandemic highlighted the precarious financial position of the French and Italian leagues due to high wage-revenue ratios and consequent operating losses
  • The financial regulation of the Bundesliga clubs put them in a much stronger position to cope with loss of revenues during the pandemic.

The top tiers of the domestic football leagues in England, France, Germany, Italy and Spain constitute the so-called “Big Five” of European football in financial terms as measured by the total revenues of their member clubs. Figure 1 shows the growth in revenues in the Big Five since 1996. The most striking feature of this timeplot is the divergent growth paths of the Big Five. From a starting point of relative parity in 1996 the divergent growth paths of the Big Five call into question whether it is even appropriate to still talk in terms of the Big Five. Using the coefficient of variation (CoV) as a measure of relative dispersion (effectively CoV is just a standardised standard deviation with the scale effect removed), the degree of dispersion between the revenues of the Big Five has more than doubled from 0.244 in 1996 to 0.509 in 2022. The English Premier League (EPL) is quite literally in a league of its own in financial terms with total revenues of €6.4bn in 2022. The rest of the Big Five lag a long way behind with the Spanish La Liga and German Bundesliga grossing revenues of €3.3bn and €3.1bn, respectively in 2022 and the Italian Serie A and French Ligue 1 lagging another €1bn or so behind with revenues of €2.4bn and €2.0bn, respectively. And with the expected uplift in the EPL’s next media rights deal and the continued growth in gate attendances, the gap between the EPL and the rest of the Big Five looks set to increase further.

Figure 1: Revenues (€m), European Big Five, 1996 – 2022

Another key feature of Figure 1 is the impact of the Covid pandemic on league revenues. The biggest losers in 2020 were the EPL clubs with the postponement of the last part of the 2019/20 leading to an overall loss of revenue of around €0.7bn. But although the whole of the 2020/21 season was played behind closed doors wiping out matchday revenues, media revenues increased with all games shown live. By 2022 with the return of spectators to football grounds and continued growth in media revenues, the EPL was back on its pre-pandemic trend with revenues over 10% higher than in 2019 prior to the pandemic. In contrast, of the other Big Five, only the French Ligue 1 had increased revenues in 2022 above the pre-pandemic level.

In assessing the revenue performance of football leagues/clubs, apart from revenue growth rates, there are two very useful revenue KPIs (Key Performance Indicators):

Media% = media revenues as a % of total revenues; and

Local Spend = non-media revenues per capita (using average league gate attendances as the size measure to standardise club/league revenues)

Media% shows the dependency of the league and its clubs on the value of their media rights. Local Spend is a measure of the marketing efficiency of clubs in generating matchday and commercial revenues relative to the size of their active fanbase as measured by average league gate attendance. As can be seen in Table 1 which reports these two revenue KPIs for 2019, 2021 and 2022, all the Big Five became much more dependent on media revenues during the Covid years as seen in the increased Media% in 2021. As would be expected Local Spend fell sharply in the Covid years with the loss of matchday revenues. What is more concerning in the longer term for the rest of the Big Five is that the financial strength of the EPL is based not only on the much higher value of their media rights but also the stronger capability of EPL clubs to generate matchday revenues and commercial revenues. Prior to the pandemic only the Spanish La Liga got close to the EPL in terms of Local Spend but by 2022 the EPL had a substantial lead over all of the other Big Five in Local Spend. Given as noted earlier, the underlying upward trends in gate attendances and the value of media rights in the EPL, when you also allow for the marketing efficiency advantage as measured by Local Spend, the financial dominance of the EPL seems likely to grow unabated in the coming years.

Table 1: Revenue KPIs, European Big Five, Selected Years

LeagueMedia%Local Spend (€)
201920212022201920212022
England59.12%68.66%54.14%3,1312,1893,732
France47.37%51.80%35.98%2,1921,7272,879
Germany44.33%55.21%43.82%2,1431,6462,164
Italy58.52%69.92%56.94%2,0491,3831,842
Spain54.25%67.74%58.53%2,8711,6472,354

 The financial strength of the EPL allows their clubs to offer lucrative salaries and pay high transfer fees to attract the best players in the global football players’ labour market. As can be seen in Figure 2, the divergent revenue growth paths of the Big Five in Figure 1 are replicated in similar divergent wage growth paths. Effectively, the €3bn revenue advantage of the EPL in 2022 allowed EPL clubs to spend €2bn more on wage costs than the German Bundesliga, the next biggest spenders in the Big Five. And it is not just the best players that can be attracted to the EPL, it is also the best coaching and support staff. The danger of financial dominance in pro team sports is that it can lead to sporting dominance and this, in turn, can undermine the sustainability of the league as teams with less financial power seek to remain competitive by overspending on wages, leading to operating losses and increasing levels of debt.

Figure 2: Wage Costs (€m), European Big Five, 1996 – 2022

 

The danger of overspending on wage costs relative to revenues can be seen very clearly in the wage-revenue ratio, possibly the most important financial performance ratio in pro team sports. By far the most dominant cost in any people business such as sport and entertainment is wages. If wage costs are too high relative to revenues, teams will make operating losses and will require to be either deficit-financed by their owners or debt-financed with all of the attendant risks. As can be seen in Figure 3, the wage-revenue ratios have tended to be highest in the French and Italian leagues, the smallest financially of the Big Five leagues. Indeed in the early 2000s the Italian Serie A got close to spending all of its revenue on wages, with the French Ligue 1 nearly emulating this during the Covid years.

Figure 3: Wage-Revenue Ratios, European Big Five, 1996 – 2022

Table 2 shows the danger of the financially smaller leagues having higher wage-revenue ratios. They can be put in a very precarious position if there is a sudden loss of revenues as happened during the pandemic (but could also happen if there is a loss in the value of a league’s media rights). Wage costs are largely fixed at any point in time through contractual commitments so any reduction in revenues is likely to lead to higher wage-revenue ratios and operating losses. As a benchmark, financial prudence would normally dictate wage-revenue under 65% in order to make operating profits. The French and Italian leagues operated with wage-revenue ratios above 70% prior to the pandemic and both remained above 80% in 2022. The Spanish La Liga was on a par with the EPL in 2019 at just over 60%. Both leagues saw their wage-revenue ratio rise above 70% in 2021 but, whereas the EPL fell back below 67% in 2022, La Liga remained high above 70%.

Table 2: Wage-Revenue Ratio, European Big Five, Selected Years

LeagueWage-Revenue Ratio
201920212022
England61.17%71.05%66.84%
France73.03%98.27%86.87%
Germany53.75%64.96%59.13%
Italy70.42%82.98%82.98%
Spain62.04%74.19%72.66%

In footballing terms, the bastion of football prudence has been the German Bundesliga with its longstanding financial management regime requiring clubs to submit budgets for approval as a condition of their league membership. As seen in both Figure 3 and Table 2, the Bundesliga has historically operated with wage-revenue ratios between 45% and 55%. Even with the loss of revenue during the Covid years, the wage-revenue ratio only hit 65% and fell back below 60% in 2022. The effectiveness of the German approach can be seen in Table 3 which reports the marginal wage-revenue ratio (MWRR) over the last 27 years. What this ratio shows is the proportion on average spent on wages of every increment of €1m of revenue over the last 27 years as each league has grown financially. The EPL has had a MWRR of 65.0% with the Spanish La Liga operating in a very similar way with a MWRR of 67.7%. The Bundesliga has had a MWRR of 56.5%. Given that the Spanish and German leagues are of a similar size in revenue terms, it suggests that long term the Germen financial management regime has lowered their wage-revenue ratio by 11% compared to what it would have been with a lighter touch. The very high MWRRs of the French and Italian leagues coupled with their lower revenue growth rates further reinforce the concerns over their financial future.

Table 3: Marginal Wage-Revenue Ratio, European Big Five, 1996 – 2022

LeagueMarginal Wage-Revenue Ratio 1996 – 2022
England65.03%
France83.21%
Germany56.60%
Italy79.31%
Spain67.73%

Notes:

  1. The raw financial data for the analysis has been sourced from various editions of Deloitte’s Annual Review of Football Finance (Annual Review of Football Finance 2023 | Deloitte Global)
  2. Throughout the years refer to financial year-end. Hence, for example, the figures reported for 1996 refer to season 1995/96.
  3. The base year of 1996 has been used since 1995/96 was the first season when the EPL adopted its current 20-club, 380-game format.
  4. Average league gates for season 2019/20 have been used to calculate Local Spend during the Covid years when games were played behind closed doors with no spectators in the stadia.

Analytics and Context

Executive Summary

  • Context is crucial in data analytics because the purpose of data analytics is always practical to improve future performance
  • The context of a decision is the totality of the conditions that constitute the circumstances of the specific decision
  • The three key characteristics of the context of human behaviour in a social setting are (i) uniqueness; (ii) “infinitiveness”; and (iii) uncertainty
  • There are five inter-related implications for data analysts if they accept the critical importance of context:

Implication 1: The need to recognise that datasets and analytical models are always human-created “realisations” of the real world.

Implication 2: All datasets and analytical models are de-contextualised abstractions.

Implication 3: Data analytics should seek to generalise from a sample rather than testing the validity of universal hypotheses.

Implication 4: Given that every observation in a dataset is unique in its context, it is vital that exploratory data analysis investigates whether or not a dataset fulfils the similarity and variability requirements for valid analytical investigation.

Implication 5: It is misleading to consider analytical models as comprising dependent and independent variable

As discussed in a previous post, “What is data analytics?” (11th Sept 2023), data analytics is best defined as data analysis for practical purpose. The role of data analytics is to use data analysis to provide an evidential basis for managers to make evidence-based decisions on the most effective intervention to improve performance. Academics do not typically do data analytics since they are mostly using empirical analysis to pursue disciplinary, not practical, purposes. As soon as you move from disciplinary purpose to practical purpose, then context becomes crucial. In this post I want to explore the implications for data analytics of the importance of context.

              The principal role of management is to maintain and improve the performance levels of the people and resources for which they are responsible. Managers are constantly making decisions on how to intervene and take action to improve performance. To be effective, these decisions must be appropriate given the specific circumstances that prevail. This is what I call the “context” of the decision – the totality of the conditions that constitute the circumstances of the specific decision.

              In the case of human behaviour in a social setting, there are three key characteristics of the context:

  1.   Unique

Every context is unique. As Heraclitus famously remarked, “You can never step into the same river twice”. You as an individual will have changed by the time that you next step into the river, and the river itself will also have changed – you will not be stepping into the same water in the exactly the same place. So too with any decision context; however similar to previous decision contexts, there will some unique features including of course that the decision-maker will have experience of the decision from the previous occasion. In life, change is the only constant. From this perspective, there can never be universality in the sense of prescriptions on what to do for any particular type of decision irrespective of the specifics of the particular context. A decision is always context-specific and the context is always unique. 

2. “Infinitive”

By “infinitive” I mean that there are an infinite number of possible aspects of any given decision situation. There is no definitive set of descriptors that can capture fully the totality of the context of a specific decision.

3. Uncertainty

All human behaviour occurs in the context of uncertainty. We can never fully understand the past which will always remain contestable to some extent with the possibility of alternative explanations and interpretations. And we can never know in advance the full consequences of our decisions and actions because the future is unknowable. Treating the past and future as certain or probabilistic disguises but does not remove uncertainty. Human knowledge is always partial and fallible

              Much of the failings of data analytics derive from ignoring the uniqueness, “infinitiveness” and uncertainty of decision situations. I often describe it as the “Masters of the Universe” syndrome – the belief that because you know the numbers, you know with certainty, almost bordering on arrogance, what needs be done and all will be well with world if only managers would do what the analysts tell them to do. This lack of humility on the part of analysts puts managers offside and typically leads to analytics being ignored. Managers are experts in context. Their experience has given them an understanding, often intuitive, of the impact of context. Analysts should respect this knowledge and tap into it. Ultimately the problem lies in treating social human beings who learn from experience as if they behave in a very deterministic manner similar to molecules. The methods that have been so successful in generating knowledge in the natural sciences are not easily transferable to the realm of human behaviour. Economics has sought to emulate the natural sciences in adopting a scientific approach to the empirical testing of economic theory. This has had an enormous impact, sometimes detrimental, on the mindset of data analysts given that a significant number of data analysts have a background in economics and econometrics (i.e. the application of statistical analysis to study of economic data).

              So what are the implications if we as data analysts accept the critical importance of context? I would argue there are five inter-related implications:

Implication 1: The need to recognise that datasets and analytical models are always human-created “realisations” of the real world.

The “infinitiveness” of the decision context implies that datasets and analytical models are always partial and selective. There are no objective facts as such. Indeed the Latin root of the word “fact” is facere (“to make”). Facts are made. We frame the world, categorise it and measure it. Artists have always recognised that their art is a human interpretation of the world. The French impressionist painter, Paul Cezanne, described his paintings as “realisations” of the world. Scientists have tended to designate their models of the world as objective which tends to obscure their interpretive nature. Scientists interpret the world just as artists do, albeit with very different tools and techniques. Datasets and analytical models are the realisations of the world by data analysts.

Implication 2: All datasets and analytical models are de-contextualised abstractions.

As realisations, datasets and analytical models are necessarily selective, capturing only part of the decision situation. As such they are always abstractions from reality. The observations recorded in a dataset are de-contextualised in the sense that they are abstracted from the totality of the decision context.

Implication 3: Data analytics should seek to generalise from a sample rather that testing the validity of universal hypotheses.

There are no universal truths valid across all contexts. The disciplinary mindset of economics is quite the opposite. Economic behaviour is modelled as constrained optimisation by rational economic agents. Theoretical results are derived formally by mathematical analysis and their validity in specific contexts investigated empirically, in much the same way as natural science uses theory to hypothesise outcomes in laboratory experiments. Recognising the unique, “infinitive” and uncertain nature of the decision context leads to a very different mindset, one based on intellectual humility and the fallibility of human knowledge. We try to generalise from similar previous contexts to unknown, yet to occur, future contexts. These generalisations are, by their very nature, uncertain and fallible.

Implication 4: Given that every observation in a dataset is unique in its context, it is vital that exploratory data analysis investigates whether or not a dataset fulfils the similarity and variability requirements for valid analytical investigation.

Every observation in a dataset is an abstraction from a unique decision context. One of the critical roles of the Exploration stage of the analytics process is to ensure that the decision contexts of each observation are sufficiently similar to be treated as a single collective (i.e. sample) to be analysed. The other side of the coin is checking the variability. There needs to be enough variability between the decision contexts so that the analyst can investigate which aspects of variability in the decision contexts are associated with the variability in the observed outcomes. But if the variability is excessive, this may call into question the degree of similarity and whether or not it is valid to assume that all of the observations have been generated by the same general behaviour process. Excessive variability (e.g. outliers) may represent different behavioural processes, requiring the dataset to be analysed as a set of sub-samples rather than as a single sample.

Implication 5: It can be misleading to consider analytical models as comprising dependent and independent variables.

Analytical models are typically described in statistics and econometrics as consisting of dependent and independent variables. This embodies a rather mechanistic view of the world in which the variation of observed outcomes (i.e. the dependent variable) is to be explained by the variation in the different aspects of the behavioural process as measured (or categorised) by the independent variables. But in reality these independent variables are never completely independent of each other. They share information (often known as “commonality”) to the extent that for each observation the so-called independent variables are extracted from the same context. I prefer to think of the variables in a dataset as situational variables – they attempt to capture the most relevant aspects of the unique real-world situations from which the data has been extracted but with no assumption that they are independent; indeed quite the opposite. And, given the specific practical purpose of the particular analytics project, one or more of these situational variables will be designated as outcome variables.

Read Other Related Posts

What is Data Analytics? 11th Sept 2023

The Six Stages of the Analytics Process, 20th Sept 2023

Financial Determinism and the Shooting-Star Phenomenon in the English Premier League

Executive Summary

  • Financial determinism in professional team sports refers to those leagues in which sporting performance is largely determined by expenditure on playing talent
  • Financial determinism creates the “shooting-star” phenomenon – a small group of ”stars”, big-market teams with the high wage costs and high sporting performance, and a large “tail” of smaller-market teams with lower wage costs and lower sporting performance
  • There is a very high degree of financial determinism in the English Premier League
  • Achieving high sporting efficiency is critical for small-market teams with limited wage budgets seeking to avoid relegation

Financial determinism in professional team sports refers to those leagues in which sporting performance is largely determined by expenditure on playing talent. It is the sporting “law of gravity”. Financial determinism implies a strong win-wage relationship with league outcomes highly correlated with wage costs so that those teams with the biggest markets and the greatest economic power (i.e. the biggest “wallets”) to be able to afford the best players tend to win. Financial determinism creates what can be called the “shooting-star” phenomenon shown in Figure 1. The “stars” are the sporting elite in any league, the big-market teams with the high wage costs and high sporting performance. The rest of the league constitutes the “tail”, the smaller-market teams with lower wage costs and lower sporting performance. Some small-market teams can temporarily defy the law of gravity by achieving high sporting efficiency. The classic example of this is the Moneyball story in Major League Baseball where the Oakland Athletics used data analytics to identify undervalued playing talent. And, of course, there are the bigger market teams who spend big but do so inefficiently and perform well below expectation.

Figure 1: The Shooting-Star Phenomenon

A fundamental proposition in sports economics is that uncertainty of outcome is a necessary condition for viable professional sports leagues. This is the notion that the essential characteristic of sport is the excitement of unscripted drama where the outcome is determined by the contest and is not scripted in advance. Uncertainty of outcome requires that teams in any league are relatively equally matched in their economic power with similar revenues and similar access to financial capital. Unequal distribution of economic power across teams leads to financial determinism. The most common causes of disparities in economic power between teams are location (i.e. teams based in large metropolitan areas often have much bigger fanbases and, consequently, can generate much higher revenues) and ownership wealth (i.e. teams with rich owners who are driven by sporting glory rather than profit and will spend whatever it takes to win). To prevent financial determinism, leagues have used a number of regulatory mechanisms to maintain competitive balance including revenue sharing, salary caps and player drafts.

Is the English Premier League subject to financial determinism and the shooting-star phenomenon? To answer this question I have tracked wage costs reported in club accounts from 1995/96 onwards when the English Premier League adopted its current structure of 20 teams and 380 games with three teams relegated. Clubs are still in the process of reporting their 2023 accounts so that the analysis concludes with season 2021/22. Since the analysis covers 27 seasons, wage costs need to be standardised to allow for wage inflation. I have used average wage costs each season to deflate wage costs to 1995/96 levels.  Very roughly, £10m wage costs in 1996/97 equates to £200m wage costs in 2021/22. Sporting performance has been measured by league points based on match outcomes; any point deductions for breach of league regulations have been excluded. (Middlesbrough were deducted 3 points in 1996/97 for failing to fulfil a scheduled fixture and Portsmouth were deducted 9 points in 2009/10 for going into administration.) Figure 2 shows the scatterplot of league points and standardised wage costs. The two groupings, the big-spending stars and the lower-spending tail, are very obvious. The tail is very dense and contains most of the observations (73.9% of the clubs had standardised wage costs under £10m). The stars are fewer in number and more dispersed with 10 instances of clubs having standardised wage costs in excess of £20m (which equates to over £400m in 2021/22). The correlation between standardised wage costs and league points is 0.793 which implies that over the 27 seasons, 62.8% of the variation in league performance can be explained by the variation in wage costs. In other words, there is a very high degree of financial determinism in the English Premier League.

Figure 2: The Shooting-Star Phenomenon in the English Premier League

Season 2021/22 is very typical as regards the degree of financial determinism in the English Premier League as shown in Figure 3. The correlation between wage costs and league points is 0.793 which implies that 61.2% of the variation in league performance can be explained by the variation in wage costs. The linear trendline acts as a performance benchmark – the average efficient outcome for any given level of wage costs – and thus identifies above-average efficient (“above the line”) outcomes and below-average efficient, “below the line” outcomes. At the top end, Manchester City, the champions with 93 points, a single point ahead of Liverpool, were outspent by both Manchester United and Liverpool. Manchester United were highly inefficient gaining only 58 points but with wage costs of £408m. By comparison, West Ham United gained 56 points with wage costs of £136m.

Figure 3: Win-Wage Relationship in English Premier League, 2021/22

As regards relegation, all three relegated teams – Norwich City, Watford and Burnley – lie below the average-efficiency line. In the cases of both Burnley and Watford their final league positions matched their wage rank  – their sporting efficiency was not good enough to offset their resource disadvantage. In contrast, Norwich City allocated enough resource to avoid relegation – their wage costs of £117m ranked 15th – but they were highly inefficient. Of the lower spending teams, the two most efficient teams were Brentford and Brighton and Hove Albion who both finished safely in mid-table but ranked 20th and 16th, respectively, in wage costs. In a future post, I will analyse the determinants of sporting efficiency in more detail.

Read other Related Posts

Measuring Trend Growth

Executive Summary

  • The most useful summary statistic for a trended variable is the average growth rate
  • But there are several different methods for calculating average growth rates that can often generate very different results depending on whether all the data is used or just the start and end points, and whether simple or compound growth is assumed
  • Be careful of calculating average growth rates using only the start and end points of trended variables since this implicitly assumes that these two points are representative of the dynamic path of the trended variable and may give a very biased estimate of the underlying growth rate
  • Best practice is to use all of the available data to estimate a loglinear trendline which allows for compound growth and avoids having to calculate an appropriate midpoint of a linear trendline to convert the estimated slope into  growth rate

When providing summary statistics for trended time-series data, the mean makes no sense as a measure of the point of central tendency. By definition, there is no point of central tendency in trended data. Trended data are either increasing or decreasing in which case the most useful summary statistic is the average rate of growth/decline. But how do you calculate the average growth rate? In this post I want to discuss the pros and cons of the different ways of calculating the average growth rate, using total league attendances in English football (the subject of my previous post) as an illustration.

              There are at least five different methods of calculating the average growth rate:

  1. “Averaged” growth rate: use gt = (yt – yt-1)/yt-1 to calculate the growth rate for each period then average these growth rates
  2. Simple growth rate: use the start and end values of the trended variable to calculate the simple growth rate with the trended variable modelled as yt+n = yt(1 + ng)
  3. Compound growth rate: use the start and end values of the trended variable to calculate the compound growth rate with the trended variable modelled as yt+n = yt(1 + g)n
  4. Linear trendline: estimate the line of best fit for yt = a + gt (i.e. simple growth)
  5. Loglinear trendline: estimate the line of best fit for ln yt = a + gt (i.e. compound growth)

where y = the trended variable; g  = growth rate; t = time period; n = number of time periods; a = intercept in line of best fit

These methods differ in two ways. First, they differ as to whether the trend is modelled as simple growth (Methods 2, 4) or compound growth (Methods 3, 5). Method 1 is effectively neutral in this respect. Second, the methods differ in terms of whether they use only the start and end points of the trended variable (Methods 2, 3) or use all of the available data (Methods 1, 4, 5). The problem with only using the start and end points is that there is an implicit assumption that these are representative of the underlying trend with relatively little “noise”. But this is not always the case and there is a real possibility of these methods biasing the average growth rate upwards or downwards as illustrated by the following analysis of the trends in football league attendances in England since the end of the Second World War.

Figure 1: Total League Attendances (Regular Season), England, 1946/47-2022/23

This U-shaped timeplot of total league attendances in England since the end of the Second World War splits into two distinct sub-periods of decline/growth:

  • Postwar decline: 1948/49 – 1985/86
  • Current revival: 1985/86 – 2022/23

Applying the five methods to calculate the average annual growth rate of these two sub-periods yields the following results:

MethodPostwar Decline 1948/49 – 1985/86Current Revival 1985/86 – 2022/23*
Method 1: “averaged” growth rate-2.36%2.28%
Method 2: simple growth rate-1.62%3.00%
Method 3: compound growth-2.45%2.04%
Method 4: linear trendline-1.89%1.75%
Method 5: loglinear trendline-1.95%1.85%
*The Covid-affected seasons 2019/20 and 2020/21 have been excluded from the calculations of the average growth rate.

What the results show very clearly is the wide variability in the estimates of average annual growth rates depending on the method of calculation. The average annual rate of decline in league attendances between 1949 and 1986 varies between -1.62% (Method 2 – simple growth rate) to -2.45% (Method 3 – compound growth rate). Similarly the average annual rate of growth from 1986 onwards ranges from 1.75% (Method 4 – linear trendline) to 3.00% (Method 2 – simple growth rate). To investigate exactly why the two alternative methods for calculating the simple growth rate during the Current Revival give such different results, the linear trendline for 1985/86 – 2022/23 is shown graphically in Figure 2.

Figure 2: Linear Trendline, Total League Attendances, England, 1985/86 – 2022/23

As can be seen, the linear trendline has a high goodness of fit (R2 = 93.1%) and the fitted endpoint is very close to the actual gate attendance of 34.8 million in 2022/23. However, there is a relatively large divergence at the start of the period with the fitted trendline having a value of 18.2 million whereas the actual gate attendance in 1985/86 was 16.5 million. It is this divergence that accounts in part for the very different estimates of average annual growth rate generated by the two methods despite both assuming a simple growth rate model. (The rest of the divergence is due to the use of midpoint to convert the slope of the trendline into a growth rate.)

              So which method should be used? My advice is to be very wary of calculating average growth rates using only the start and end points of trended variables. You are implicitly assuming that these two points are representative of the dynamic path of the trended variable and may give a very biased estimate of the underlying growth rate. My preference is always to use all of the available data to estimate a loglinear trendline which allows for compound growth and avoids having to calculate an appropriate midpoint of a linear trendline to convert the estimated slope into a growth rate.

Read Other Related Posts

League Gate Attendances in English Football: A Historical Perspective

Executive Summary

  • The historical trends in league gate attendances in English football can be powerfully summarised visually using timeplots
  • Total league attendances peaked in 1948/49 and thereafter declined until the mid-1980s
  • League attendances across the Premier League and Football League have recovered dramatically since the mid-1980s and are now at levels last experienced in the 1950s
  • Using average gates to allow for changes in the number of clubs and matches, the  Premiership matches in 2022/23 averaged 40,229 spectators per match, the highest average gate in the top division since the formation of the Football League in 1888 

How popular are the top four tiers of English league football as a spectator sport from a historical perspective? That’s the question that I want to address in this post using timeplots to visualise the historical trends in gate attendances. I have compiled a dataset with total league attendances for every season since the Football League began in 1888. To ensure as much comparability as possible, I have included only regular-season matches and excluded post-season play-off matches. (A historical footnote – post-season playoffs to decide promotion/relegation are not a modern innovation. There were playoffs called “test matches” in the early years of the Football League after the creation of the Second Division in 1892 but these were abandoned in 1898 and replaced by automatic promotion and relegation following  a scandal when Stoke City and Burnley played out a convenient goalless draw that ensured both would be promoted.)

Total league attendances for the top four divisions are plotted in Figure 1 with three breaks: 1915/16 – 1918/19 due to the First World War, 1939/40 – 1945/46 due to the Second World War and 2020/21 due to the Covid pandemic when all matches were played behind closed doors. In addition, total attendances dropped sharply in 2019/20 due to the final part of the season being postponed and the matches eventually played behind closed doors in the case of the Premier League and Championship, and cancelled entirely in League One and League Two.

Figure 1: Total League Attendances (Regular Season), England, 1888-2023

The Football League started in 1888 with a single division of 12 clubs. Preston North End were the original “Invincibles”, completing the League and FA Cup “Double” unbeaten in the inaugural season. A second division was formed in 1892 and membership of the Football League gradually expanded so that by the outbreak of the First World War in 1914 there were 40 member clubs split equally into two divisions with automatic promotion and relegation between the two divisions. Gate attendances peaked at 12.5 million in the 1913/14 season. The Football League expanded rapidly in the years immediately after the First World War with the incorporation of the Southern League as Division 3 in 1920 and the creation of a Division 3 (North) and Division 3 (South) the following years which increased the membership to 88 clubs by 1923. Total gate attendances reached 27.9 million in season 1937/38.

Gate attendances sharply increased after the Second World War, reaching a record 41.3 million in season 1948/49 which equated to around one million fans attending Football League matches on Saturday afternoons. Although the Football League expanded its membership to its current level of 92 clubs in 1950 and reorganised the two regionalised divisions into Division 3 and Division 4 in 1958, a long-term decline in attendances had set in with attendances falling steadily from the 1950s until the mid-1980s with the exception of a brief reversal of fortune in the late 1960s attributed to a renewed love of the beautiful game after England’s 1966 World Cup victory. The decline bottomed out in 1985/86 when Football League attendances fell to only 16.5 million which represented a 60.0% decrease from the peak in 1948/49. Thereafter the story has been one of continued growth, accelerated in part by the declaration of independence of the top division in 1992 with the formation of the FA Premier League. By last season (2022/23), league attendances in the top four tiers of English football had reached 34.8 million, a level last attained in season 1954/55 – quite an incredible turnaround.

The U-shaped pattern in total league attendances since the end of the Second World War is also evident but less clearly so if we focus only on the top division (see Figure 2). In particular, the post-1966 World Cup effect is much more noticeable with attendances rising from 12.5 million in 1965/66 to 15.3 million in 1967/68 and remaining above 14 million until 1973/74, and thereafter declining to a low of 7.8 million in 1988/89. Interestingly, given that league attendances in the top division account for 40% – 50% of total attendances for the top four divisions, it is somewhat anomalous that the recovery in attendances in the top division seems to have lagged around three years behind the rest of the Football League. However, part of the explanation is the changes in the number of clubs in the top division during that period. There were 22 clubs in the top division from 1919/20 to 1986/87 but this was reduced to 21 clubs in 1987/88 and 20 clubs in 1988/89 before returning to 22 clubs in 1991/92 with the current divisional structure of a 20-club Premier League and three 24-club divisions in the Football League dating from 1995.

Figure 2: League Attendances, Top Division, England, 1946-2023

Given the variations in the number of matches with spectators in the top division across time due to the changes in the number of clubs as well as the effects of the pandemic on total attendances in the 2019/20 season, it is more useful to compare average league gates (see Figure 3). The average gate at top division matches peaked at 38,776 in 1948/49 and declined to a low of 18,856 in 1983/84 (which leads the nadir of total Football League attendances by two years). The rapid growth in Premier League attendances occurred between 1993 and 2003 with the average gate of 21,125 in 1992/93, the first season of the Premier League, increasing by 67.8% over the next 10 years to an average gate of 35,445 in 2002/03. Growth has continued thereafter so that the average gate in the Premier League reached 40,229 in 2022/23, an historical high since the formation of the Football League and 3.7% above the previous record average gate set in 1948/49.

So to answer the question I posed at the start of the post – the top tier of English league football has never been more popular as measured by gate attendances on a per match basis, and the rest of the Football League has a level of popularity not experienced since the 1950s. England has rediscovered its love of the beautiful game since the mid-1980s and not just Premiership football. And that is before considering the explosive growth in TV coverage of English league football both domestically and internationally. But that, as they say, is another ball game entirely.

Figure 3: Average Gate, Top Division, England, 1946-2023

The Problem with Outliers

Executive Summary

  • Outliers are unusually extreme observations that can potentially cause two problems:
    1. Invalidating the homogeneity assumption that all of the observations have been generated by the same behavioural processes; and
    2. Unduly influencing any estimated model of the performance outcomes
  • A crucial role of exploratory data analysis is to identify possible outliers (i.e. anomaly detection) to inform the modelling process
  • Three useful techniques for identifying outliers are exploratory data visualisation, descriptive statistics and Marsh & Elliott outlier thresholds
  • It is good practice to report estimated models including and excluding the outliers in order to understand their impact on the results

A key function of the Exploratory stage of the analytics process is to understand the distributional properties of the dataset to be analysed. Part of the exploratory data analysis is to ensure that the dataset meets both the similarity and variability requirements. There must be sufficient similarity in the data to make it valid to treat the dataset as homogeneous with all of the observed outcomes being generated by the same behavioural processes (i.e. structural stability). But there must also be enough variability in the dataset both in the performance outcomes and the situational variables potentially associated with the outcomes so that relationships between changes in the situational variables and changes in performance outcomes can be modelled and investigated.

Outliers are unusually extreme observations that call into question the homogeneity assumption as well as potentially having an undue influence on any estimated model. It may be that the outliers are just extreme values generated by the same underlying behavioural processes as the rest of the dataset. In this case the homogeneity assumption is valid and the outliers will not bias the estimated models of the performance outcomes. However, the outliers may be the result of very different behavioural processes, invalidating the homogeneity assumption and rendering the estimated results of limited value for actionable insights. The problem with outliers is that we just do not know whether or not the homogeneity assumption is invalidated. So it is crucial that the exploratory data analysis identifies possible outliers (what is often referred to as “anomaly detection”) to inform the modelling strategy.

The problem with outliers is illustrated graphically below. Case 1 is the baseline with no outliers. Note that the impact (i.e. slope) coefficient of the line of best fit is 1.657 and the goodness of fit is 62.9%.

Case 2 is what I have called “homogeneous outliers” in which a group of 8 observations have been included that have unusually high values but have been generated by the same behavioural process as the baseline observations. In other words, there is structural stability across the whole dataset and hence it is legitimate to estimate a single line of best fit. Note that the inclusion of the outliers slightly increases the estimated impact coefficient to 1.966  but the goodness of fit increases substantially to 99.6%, reflecting the massive increase in the variance of the observations “explained” by the regression line.

Case 3 is that of “heterogeneous outliers” in which the baseline dataset has now been expanded to include a group of 8 outliers generated by a very different behavioural process. The homogeneity assumption is no longer valid so it is inappropriate to model the dataset with a single line of best fit. If we do so, then we find that the outliers have an undue influence with the impact coefficient now estimated to be 5.279, more than double the size of the estimated impact coefficient for the baseline dataset excluding the outliers. Note that there is a slight decline in the goodness of fit to 97.8% in Case 3 compared to Case 2, partly due to the greater variability of the outliers as well as the slightly poorer fit for the baseline observations of the estimated regression line.

Of course, in this artificially generated example, it is known from the outset that the outliers have been generated by the same behavioural process as the baseline dataset in Case 2 but not in Case 3. The problem we face in real-world situations is that we do not know if we are dealing with Case 2-type outliers or Case 3-type outliers. We need to explore the dataset to determine which is more likely in any given situation.

There are a number of very simple techniques that can be used to identify possible outliers. Three of the most useful are:

  1. Exploratory data visualisation
  2. Summary statistics
  3. Marsh & Elliott outlier thresholds

1.Exploratory data visualisation

Histograms and scatterplots as always should be the first step in any exploratory data analysis to “eyeball” the data and get a sense of the distributional properties of the data and the pairwise relationships between all of the measured variables.

2.Summary statistics

Descriptive statistics provide a formalised summary of the distributional properties of variables. Outliers at one tail of the distribution will produce skewness that will result n a gap between the mean and median. If there are outliers in the upper tail, this will tend to inflate the mean relative to the median (and the reverse if the outliers are in the lower tail). It is also useful to compare the relative dispersion of the variables. I always include the coefficient of variation (CoV) in the reported descriptive statistics.

CoV = Standard Deviation/Mean

CoV uses the mean to standardise the standard deviation for differences in measurement scales so that the dispersion of variables can be compared on a common basis. Outliers in any particular variable will tend to increase CoV relative to other variables.

3. Marsh & Elliott outlier thresholds

Marsh & Elliott define outliers as any observation that lies more than 150% of the interquartile range beyond either the first quartile (Q1) or the third quartile (Q3).

Lower outlier threshold: Q­1 – [1.5(Q3 – Q1)]

Upper outlier threshold: Q­3 + [1.5(Q3 – Q1)]

I have found these thresholds to be useful rules of thumb to identify possible outliers.

Another very useful technique for identifying outliers is cluster analysis which will be the subject of a later post.

So what should you do if the exploratory data analysis indicates the possibility of outliers in your dataset? As the artificial example illustrated, outliers (just like multicollinearity) need not necessarily create a problem for modelling a dataset. The key point is that exploratory data analysis should alert you to the possibility of problems so that you are aware that you may need to take remedial actions when investigating the multivariate relationships between outcome and situational variables at the Modelling stage. It is good practice to report estimated models including and excluding the outliers in order to understand their impact on the results. If there appears to be a sizeable difference in one or more of the estimated coefficients when the outliers are included/excluded, then you should formally test for structural instability using F-tests (often called Chow tests). Testing for structural stability in both cross-sectional and longitudinal/time-series data will be discussed in more detail in a future post. Some argue to drop outliers from the dataset but personally I am loathe to discard any data which may contain useful information. Knowing the impact of the outliers on the estimated coefficients can be useful information and, indeed, it may be that further investigation into the specific conditions of the outliers could prove to be of real practical value.

The two main takeaway points are that (1) a key component of exploratory data analysis should always be checking for the possibility of outliers; and (2) if there are outliers in the dataset, ensure that you investigate their impact on the estimated models you report. You must avoid providing actionable insights that have been unduly influenced by outliers that are not representative of the actual situation with which you are dealing.

Read Other Related Posts

The Reep Fallacy

Executive Summary

  • Charles Reep was the pioneer of soccer analytics, using statistical analysis to support the effectiveness of the long-ball game
  • Reep’s principal finding was that most goals are scored from passing sequences with fewer than five passes
  • Hughes and Franks have shown that Reep’s interpretation of the relationship between the length of passing sequences and goals scored is flawed – the “Reep fallacy” of analysing only successful outcomes
  • Reep’s legacy for soccer analytics is mixed; partly negative because of its association with a formulaic approach to tactics but also positive legacy in developing a notational system, demonstrating the possibilities for statistical analysis football and having a significant impact on practitioners

There have been long-standing “artisan-vs-artist” debates over how the “the beautiful game” (i.e. football/soccer) should be played. In his history of tactics in football, Wilson (Inverting the Pyramid, 2008) characterised tactical debates as involving two interlinked tensions – aesthetics vs results and technique vs physique. Tactical debates in football have often focused on the relative merits of direct play and possession play. And the early developments in soccer analytics pioneered by Charles Reep were closely aligned with support for direct play (i.e. “the long-ball game”).

Charles Reep (1904 – 2002) trained as an accountant and joined the RAF, reaching the rank of Wing Commander. He said that his interest in football tactics began after attending a talk in 1933 by Arsenal’s captain, Charlie Jones. Reep developed his own notational system for football in the early 1950s. His first direct involvement with a football club was as part-time advisor to Brentford in spring 1951, helping them to avoid relegation from Division 1. (And, of course, these days Brentford are still pioneering the use of data analytics to thrive in the English Premier League on a relatively small budget.) Reep’s key finding was that most goals are scored from fewer than three passes. His work subsequently attracted the interest of Stan Cullis, manager in the 1950s of a very successful Wolves team. Reep published a paper (jointly authored with Benjamin) on the statistical analysis of passing and goals scored in 1968. He analysed nearly 2,500 games during his lifetime.

In their 1968 paper, Reep and Benjamin analysed 578 matches, mainly in Football League Division 1 and World Cup Finals between 1953 and 1967. They reported five key findings:

  • 91.5% of passing sequences have 3 completed passes or less
  • 50% of goals come from moves starting in the shooting area
  • 50% of shooting-area origin attacks come from regained possessions
  • 50% of goals conceded come from own-half breakdowns
  • On average, one goal is scored for every 10 shots at goal

Reep published another paper in 1971 on the relationship between shots, goals and passing sequences that excluded shots and goals that were not generated from a passing sequence. These results confirmed his earlier analysis with passing sequences of 1 – 4 passes accounted for 87.6% of shots and 87.0% of goals scored. The tactical implications of Reep’s analysis seemed very clear – direct play with few passes is the most efficient way of scoring goals. Reep’s analysis was very influential. It was taken up by Charles Hughes, FA Director of Coaching and Education, who later conducted similar data analysis to that of Reep with similar results (but never acknowledged his intellectual debt to Reep). On the basis of his analysis, Hughes advocated sustained direct play to create an increased number of shooting opportunities.

Reep’s analysis was re-examined by two leading professors of performance analysis, Mike Hughes and Ian Franks, in a paper published in 2005. Hughes and Franks analysed 116 matches from the 1990 and 1994 World Cup Finals. They accepted Reep’s findings that around 80% of goals scored result from passing sequences of three passes or less. However, they disagreed with Reep’s interpretation of this empirical regularity as support for the efficacy of a direct style of play. They argued that it is important to take account of the frequency of different lengths of passing sequences as well as the frequency of goals scored from different lengths of passing sequences. Quite simply, since most passing sequences have fewer than five passes, it is no surprise that most goals are scored from passing sequences with fewer than five passes. I call this the “Reep fallacy” of only considering successful outcomes and ignoring unsuccessful outcomes. It is surprising how often in different walks of life people commit a similar fallacy by drawing conclusions from evidence of successful outcomes while ignoring the evidence of unsuccessful outcomes. Common sense should tell us that there is a real possibility of biased conclusions when you consider only biased evidence. Indeed Hughes and Franks found a tendency for scoring rates to increase as passing sequences get longer with the highest scoring rate (measured as goals per 1,000 possessions) occurring in passing sequences with six passes. Hughes and Franks also found that longer passing sequences (i.e. possession play) tend to produce more shots at goal but conversion rates (shots-goals ratio) are better for shorter passing sequences (i.e. direct play). However, the more successful teams are better able to retain possession with more longer passing sequences and better-than-average conversion rates.

Reep remains a controversial figure in tactical analysis because of his advocacy of long-ball tactics. His interpretation of the relationship between the length of passing sequences and goals scored has been shown to be flawed, what I call the Reep fallacy of analysing only successful outcomes. Reep’s legacy to sports analytics is partly negative because of its association with a very formulaic approach to tactics. But Reep’s legacy is also positive. He was the first to develop a notational system for football and to demonstrate the possibilities for statistical analysis in football. And, crucially, Reep showed how analytics could be successfully employed by teams to improve sporting performance.

Competing on Analytics

Executive Summary

  • Tom Davenport, the management guru on data analytics, defines analytics competitors as organisations committed to quantitative, fact-based analysis
  • Davenport identifies five stages in becoming an analytical competitor: Stage 1: Analytically impaired Stage 2: Localised analytics Stage 3: Analytical aspirations Stage 4: Analytical companies Stage 5: Analytical competitors
  • In Competing on Analytics: The New Science of Winning, Davenport and Harris identify four pillars of analytical competition: distinctive capability; enterprise-wide analytics; senior management commitment; and large-scale ambition
  • The initial actionable insight that data analytics can help diagnose why an organisation is currently underperforming and prescribe how its future performance can be improved is the starting point of the analytical journey

Over the last 20 years, probably the leading guru on the management of data analytics in organisations has been Tom Davenport. He came to prominence with his article “Competing on Analytics” (Harvard Business Review, 2006) followed up in 2007 by the book, Competing on Analytics: The New Science of Winning (co-authored with Jeanne Harris). Davenport’s initial study focused on 32 organisations that had committed to quantitative, fact-based analysis, 11 of which he designated as “full-bore analytics competitors”. He identified three key attributes of analytics competitors:

  • Widespread use of modelling and optimisation
  • An enterprise approach
  • Senior executive advocates

Davenport found that analytics competitors had four sources of strength – the right focus, the right culture, the right people and the right technology. In the book, he distilled these characteristics of analytic competitors into the four pillars of analytical competition:

  • Distinctive capability
  • Enterprise-wide analytics
    • Senior management commitment
  • Large-scale ambition

Davenport identifies five stages in becoming an analytical competitor:

  • Stage 1: Analytically impaired
  • Stage 2: Localised analytics
  • Stage 3: Analytical aspirations
  • Stage 4: Analytical companies
  • Stage 5: Analytical competitors

Davenport’s five stages of analytical competition

Stage 1: Analytically Impaired

At Stage 1 organisations make negligible use of data analytics. They are not guided by any performance metrics and are essentially “flying blind”. What data they have are poor quality, poorly defined and unintegrated. Their analytical journey starts with the question of what is happening in their organisation that provides the driver to get more accurate data to improve their operations. At this stage, the organisational culture is “knowledge-allergic” with decisions driven more by gut-feeling and past experience rather than evidence.

Stage 2: Localised Analytics

Stage 2 sees analytics being pioneered in organisations by isolated individuals concerned with improving performance in those local aspects of the organisation’s operations with which they are most involved. There is no alignment of these initial analytics projects with overall organisational performance. The analysts start to produce actionable insights that are successful in improving performance. These local successes begin to attract attention elsewhere in the organisation. Data silos emerge with individuals creating datasets for specific activities and stored in spreadsheets. There is no senior leadership recognition at this stage of the potential organisation-wide gains from analytics.

Stage 3: Analytical Aspirations

Stage 3 in many ways marks the “big leap forward” with organisations beginning to recognise at a senior leadership level that there are big gains to be made from employing analytics across all of the organisation’s operations. But there is considerable resistance from managers with no analytics skills and experience who see their position as threatened. With some senior leadership support there is an effort to create more integrated data systems and analytics processes. Moves begin towards a centralised data warehouse managed by data engineers.

Stage 4: Analytical Companies

By Stage 4 organisations are establishing a fact-based culture with broad senior leadership support. The value of data analytics in these organisations is now generally accepted. Analytics processes are becoming embedded in everyday operations and seen as an essential part of “how we do things around here”. Specialist teams of data analysts are being recruited and managers are becoming familiar with how to utilise the results of analytics to support their decision making. There is a clear strategy on the collection and storage of high-quality data centrally with clear data governance principles in place.

Stage 5: Analytical Competitors

At Stage 5 organisations are now what Davenport calls “full-bore analytical competitors” using analytics not only to improve current performance of all of the organisation’s operations but also to identify new opportunities to create new sustainable competitive advantages. Analytics is seen as a primary driver of organisational performance and value. The organisational culture is fact-based and committed to using analytics to test and develop new ways of doing things.

To quote an old Chinese proverb, “a thousand-mile journey starts with a single step”. The analytics journey for any organisation starts with an awareness that the organisation is underperforming and data analytics has an important role in facilitating an improvement in organisational performance. The initial actionable insight that data analytics can help diagnose why an organisation is currently underperforming and prescribe how its performance can be improved in the future is the starting point of the analytical journey.

Read Other Related Posts

What Can Football and Rugby Coaches Learn From Chess Grandmasters?

Executive Summary

  • Set plays in invasion-territorial team sports can be developed and practiced in advance as part of the team’s playbook and put the onus on the coach to decide the best play in any given match context
  • Continuous open play with multiple transitions between attack and defence puts the onus on the players to make instant ball play and positioning decisions
  • The 10-year/10,000-hours rule to become an expert has been very influential in planning the long-term development of players and derives ultimately from the understanding of the perception skills of chess grandmasters
  • Chess grandmasters acquire their expertise in practical problem-solving by spending thousands of hours studying actual match positions and evaluating the moves made
  • Improved decision-making should be a key learning outcome in all training sessions involving open play under match conditions

Player development in football, rugby and the other invasion-territorial team sports is a complex process. Expertise in these types of sports is very multi-dimensional so that increasingly coaches are moving away from a concentration on just technical skills and fitness to embrace a more holistic approach. The English FA advocates the Four-Corner Model (Technical, Physical, Psychological and Social) as a general framework for guiding the development pathway of all players regardless of age or ability. I prefer to think in terms of the four A’s – Ability, Athleticism, Attitude and Awareness – in order to highlight the importance of decision making i.e. awareness of the “right” thing to do in any given match situation. My basic question is whether or not coaches in football and rugby put enough emphasis on the development of the decision-making skills of players.

Players have to make a myriad of instant decisions in a match, particularly in those invasion-territorial team sports characterised by continuous open play. At one extreme is American football which is effectively a sequence of one-phase set plays that can be choreographed in advance and mostly puts the onus for in-game decision-making on the coaches not the players. The coach writes a detailed script and players have to learn their lines exactly with little room for improvisation. By contrast (association) football is at the opposite end of the spectrum with few set plays and mostly open play with continuous transition between attack and defence; in other words, continuous improvisation. Rugby union has more scope for choreographed set plays at lineouts and scrums but thereafter the game transitions into multi-phase open play. Continuous open play puts the onus firmly on players rather than coaches for in-game decision-making. Players must continuously decide on their optimal positioning as well as making instant decisions on what to do with the ball when they are in possession. This demands ultra-fast expert problem-solving abilities to make the right choice based on an acute sense of spatial awareness.

How can football and rugby coaches facilitate the development of ultra-fast expert problem-solving abilities? One possible source of guidance is chess, an area of complex problem-solving that has been researched extensively and has thrown up important and sometimes surprising insights into the nature of expertise. The traditional view has been that grandmasters in chess are extraordinarily gifted calculators with almost computer-like abilities to very quickly consider the possible outcomes of alternative moves, able to project the likely consequences many moves ahead. But, starting with the pioneering research in the 1950s/60s of, amongst others, De Groot and Herbert Simon, a psychologist who won the Nobel Prize for Economics, we now have a very different view of what makes a grandmaster such an effective problem solver. Four key points have emerged from the research on perception in chess:

  1. Chess grandmasters do not undertake more calculations than novices and intermediate-ability players. If anything grandmasters make fewer calculations but yet are much more able to intuitively select the right move.
  2. The source of expertise of chess grandmasters and masters lies in their ability to recognise patterns in games and to associate a specific pattern with an optimal move. Both De Groot and Simon tested the abilities of chess players of different standards to recall board positions after a very brief viewing. In the case of mid-game positions from actual games with 24 – 26 pieces on the board, masters were able to correctly recall around 16 pieces on their first attempt whereas intermediate-ability players averaged only eight pieces and novices just four pieces. Yet when confronted with 24 – 26 pieces randomly located on the board, there was virtually no difference in the recall abilities between players of different playing abilities with all players averaging only around four pieces correctly remembered. There is a logic to the positioning of pieces in actual games which expert players can appreciate and exploit in retrieving similar patterns from games stored in their long-term memory and identifying the best move. This competitive advantage disappears when pieces are located randomly and, by definition, can never have any relevant precedents for guidance.
  3. Further investigation shows that expert chess players store board positions in their memories as “chunks” consisting of around three mutually related pieces with pieces related by defensive dependency, attacking threats, proximity, colour or type. Since there is a logic to how pieces are grouped in memory chunks, grandmasters tend to need fewer chunks to remember a board position compared to lesser players.
  4. Simon estimated that a grandmaster needs at least 50,000 chunks of memory of patterns from actual games but probably many more and that this would require at least 10 years (or 10,000 hours) of constant practice.

The 10-year/10,000-hours rule to become an expert is now very widely known amongst coaches and indeed has been very influential in planning the long-term development of athletes. Much of the recent popularisation of the 10-year/10,000-hours rule is associated with Ericsson’s work on musical expertise. What is often forgotten is that Ericsson was originally inspired by Simon’s work in chess and indeed Ericsson went on to study under Simon. So our understanding of problem-solving in chess is already having an impact on player development in team sports albeit largely unacknowledged.

Chess grandmasters acquire their expertise in practical problem-solving by spending thousands of hours studying actual match positions and evaluating the moves made. Football and rugby coaches responsible for player development need to ask themselves if their coaching programmes are allocating enough time to developing game-intelligence in open play under match conditions. Not only do players need to analyse the videos of their own decision-making in games but they also need to build up their general knowledge of match positions and the decision-making of top players by continually studying match videos. And this analysis of decision-making should not be limited to the classroom. Improved decision-making should be a key learning outcome in all training sessions involving open play under match conditions.

Note

This post was originally written in June 2016 but never published. It may seem a little dated now but I think the essential insights remain valid. I am a qualified football coach (UEFA B License) and coached for several years from Under 5s through to college level before concentrating on providing data analysis to coaches. I have always considered my coaching experience to have been a key factor in developing effective analyst-coach relationships at the various teams with which I have worked.